Vídeo de elementos naturales en los que se da la proporción áurea
Donald en la tierra mágica de la matemática
| La proporción áurea
Una proporción es la relación entre dos razones, una comparación entre dos razones. Euclides estableció la proporción áurea mediante la división de un segmento por un punto dado de manera que la línea o segmento entero respecto al segmento medio de la división es igual a la relación entre el segmento medio y el menor de la división. El cociente entre cada par de razones es de forma aproximada 1,61803. Se puede expresar también mediante uno más/menos (en su otra solución) raíz de cinco partido dos. Si al segmento medio lo llamamos x y al menor uno, como tenemos que la línea se separa en extrema y media razón, x es a uno como uno más x es a x.
X/1=(x + 1)/x
Despejando tenemos que x al cuadrado menos x menos 1 es igual a 0, esta ecuación de segundo grado se resuelve de la siguiente forma: x igual a menos b más menos, raíz cuadrada de b al cuadrado menos 4 por a y por c partido todo por dos por a; siendo a, b, c los tres términos de la ecuación, 1º, 2º y 3º respectivamente.
Cuando phi es positivo el valor es 1,6180339887, también llamado nº de oro.
A continuación mostramos algunos decimales correspondientes al número de oro (valor del cociente entre dos segmentos de la proporción): 1,61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 28621 35448 62270 52604 62818 90244 97072 07204 18939 11374 Si elevamos al cuadrado el número de oro tenemos el mismo número más la unidad: 1,61803 al cuadrado = 2,61803 Si dividimos uno entre el número de oro , obtenemos 0,618 que es la otra solución a la ecuación de segundo grado, sin tener en cuenta el negativo de la misma:
1/1,61803= 0,61803
La proporción áurea no se puede expresar como un número racional, no se puede obtener un número común que este contenido equis veces en el segmento medio y otro número de veces en el segmento menor, por esto se llaman longitudes inconmensurables, y son aquellas que no contienen medidas comunes.

Existe una relación de proporción en la que se cumple que un segmento mayor a+b es al medio a como el medio a es al menor b, al tiempo que la suma del segmento medio a y menor b es igual al segmento mayor (a +b), a esta relación de proporción se le llama áurea.
En el dibujo podemos verificar que esto es cierto, se trata de demostrar que el segmento mayor (a +b), es al medio a como éste al menor b y la suma del medio a y el menor b es igual al mayor (a +b). Para ello proyectamos el segmento mayor (a +b) sobre otro segmento “medio” c (que es igual a a), al proyectar mediante una recta paralela el segmento medio a sobre el mismo segmento obtenemos otro segmento d que es igual al menor d, de esta forma observamos que el segmento mayor es al medio como el medio es al menor y al tiempo la suma del medio y menor es igual al mayor.
Para mayor claridad se ha concretado de forma numérica dando al segmento medio el valor uno. De esta forma al dividir el segmento mayor entre uno sabemos que va a dar el valor del número áureo, con lo que estamos obligados a considerar el segmento mayor con el valor de 1,618. La diferencia de ambos provoca que el segmento menor sea 0,618. El mayor entre el medio tiene como cociente 1,618 y análogamente el medio entre el menor tiene el mismo valor.
Si cambiamos los términos de la proporción tenemos que (a+b)/a=a/b se transforma en b/a=a/(a+b), tenemos por tanto que 0,618 es a uno, como uno es 1,618. En este caso el cociente entre ambos términos es 0,618, el otro valor de la ecuación de segundo grado que no se utiliza por tener signo negativo.

Podemos comprobar que la relación que establece la proporción áurea para 2 segmentos cualesquiera a b, por regla general no se cumple. En la figura tenemos un segmento dividido en dos partes, un segmento medio b y otro menor c , la suma de ambos es igual al segmento mayor a, tenemos: (a= b+c). Gráficamente proyectamos el segmento mayor a y lo transformamos en el segmento medio b=b’, al proyectar en la misma dirección el segmento medio b observamos que se transforma en otro segmento distinto de c, diferente del menor, como exigiría la proporción áurea, con lo cual tenemos que no se verifica que el mayor es al medio como el medio es al menor.
Podemos coger un segmento, por ejemplo 13,6, y multiplicarlo por 1,618, de esta forma tenemos el segmento menor y el segmento medio. A continuación podemos por el teorema de Thales transformarlos de manera que la suma de ambos se transformen en el segmento medio y el segmento medio se transforme en el menor. Pero este detalle no nos dicen nada de cómo poder construir el número de oro, ya que partimos de su conocimiento.
Para obtenerlo podemos seguir el siguiente procedimiento:
Tenemos un segmento AB y debemos obtener otro BC que esté en proporción áurea con él. Construimos un cuadrado ABCD a partir del segmento base AB y haciendo centro en su punto medio O hacemos una circunferencia que pase por los otros dos vértices del cuadrado FD. Esta circunferencia corta a la prolongación de la base del cuadrado AB en un punto C, este punto es el del segmento BC que está en proporción áurea con el segmento dado AB. Podemos comprobar que ello es cierto aplicando el teorema de Tales pues al transformar el segmento mayor AC en el segmento medio FA del lado vertical del cuadrado igual a AB y al hacer por el punto B una paralela BH a esta dirección FC obtenemos el segmento menor HA y comprobamos que tiene la dimensión BC al trasladar mediante un giro de centro O este segmento menor BC a su nueva posición GA y al hacer centro en A la nueva circunferencia de radio GA observamos que es coincidente con el radio HA. Queda demostrado por tanto en el dibujo que el segmento mayor AC es al medio AB o FA como el medio es al menor BC o AH, siendo él mismo tiempo el segmento mayor AC igual a la suma de los otros dos AB, BC.
En la figura inferior podemos observar un cuadrado amarillo de lado b. Haciendo centro en el punto medio del lado y tomando como radio la distancia de ese punto a cualquiera de los vértices superiores, por ejemplo el punto H, hacemos un arco hasta que corta a la prolongación del lado en un punto M. Desde la conclusión del lado b a ese punto M tenemos un nuevo segmento c. El lado del cuadrado b y este nuevo segmento c están en proporción áurea. Como podemos observar los dos segmentos en proporción áurea bc suman el segmento a.
Para demostrar gráficamente que esta relación es válida, proyectamos a la parte superior del segmento total a y colocamos a su derecha y en el extremo el cuadrado amarillo de lado b. Proyectamos también el segmento c sobre la prolongación del segmento a. Haciendo centro en el punto medio del segmento a+c construimos una semicircunferencia que corta al cuadrado en el extremo superior.
Se tiene por tanto que el lado del cuadrado b es media proporcional entre el segmento a que es la suma de los dos b+c y el segmento c, queda en consecuencia demostrado gráficamente la relación que existe entre los tres segmentos, a saber: a es igual a b más c, el segmento a es al segmento b como el segmento b es al segmento c.
Si cogemos dos números cualesquiera (3 y 8, p. ej.) y los sumamos obtenemos un nuevo número 11 que lo sumamos al anterior 8 y así de forma sucesiva , después de operar con unos cuantos dividimos dos números consecutivos , el mayor entre el menor y observamos que el cociente es el valor del número de oro: 1,618 .
3 8 11 19 30 49 79 128 207 335
305 / 207 = 1’618

Si cogemos por ejemplo otros dos números cualesquiera, el dos y el cinco, observamos en el dibujo que ambos segmentos distan mucho de estar en proporción áurea , no obstante podemos observar a continuación que al empezar a sumar el último más el anterior (2 + 5, 5 + 7, 7 + 12, 19 + 12, etc.), veremos que los dos últimos de la serie que tomemos se van aproximando cada vez más a la proporción áurea.
Tomamos como ejemplo el dos y el cinco. Sumamos 2 + 5 y obtenemos siete más el anterior obtenemos 12, +7 tenemos 19, +12 obtenemos 31, +19 obtenemos 50, +31 obtenemos 81, +50 obtenemos 131, +81 obtenemos 212, de forma análoga sumando siempre los dos últimos términos obtenemos los siguientes números de la serie: 343, 555,898, 1453,2351,3804,6155, etc. Si dividimos los dos últimos de la serie tenemos como cociente el número de oro, 1,618.
En el cuadro hemos hecho una línea horizontal y hemos ido colocando de forma vertical los segmentos con su dimensión correspondiente, guardando siempre la misma distancia entre ellos. A la derecha, en los dos últimos términos de la serie (en color verde y rojo, los correspondientes a los números 6155 y 3804), podemos observar cómo estos dos segmentos están prácticamente en exacta proporción áurea, por tanto al ir sumando siempre el segmento previo al último tenemos un nuevo segmento que es cada vez con mayor aproximación proporción áurea con el anterior.
En la imagen se puede observar de forma gráfica como el último segmento dibujado a la derecha en color violeta y naranja (a mas b), se obtiene sumando el anterior azul más naranja (c mas a) más el mayor del anterior en color naranja (a).
Si retrocedemos hasta el principio podemos observar en los rectángulos que siempre tomamos para obtener el último la suma de los dos anteriores mas el mayor de los anteriores. De esta forma obtenemos siempre dos medidas que cada vez se acercan más a las que corresponden a la proporción áurea.
Phi en la naturaleza y en el arte:
La proporción áurea contiene muchas propiedades interesantes, aparece en pautas armónicas en los diseños naturales como plantas y pétalos de flores, los moluscos, los huracanes, remolinos y vientos, en la disposición de de semillas de frutas, de las estrellas, en espirales de la naturaleza, en cuernos de numerosos animales, etc. También se da en la disposición de la estructura del oído interno. En las conchas de moluscos observamos siempre una distribución en espiral en la que se da la proporción áurea, y esto ha servido para la construcción de numerosos detalles arquitectónicos, como por ejemplo los que corresponden al estilo jónico de las columnas de arquitecturas griegas.
El número de oro se da en los fósiles, en los vuelos de los halcones que caen hacia su presa haciendo un espiral logarítmica expandida de forma tridimensional para tener una mejor visión de la orientación del espacio, en los cuernos del carnero, en los colmillos del elefante, en la dinámica de los agujeros negros, en los remolinos, en la disposición de los cristales en empaquetamientos estables, en empaquetamientos de estructuras microscópicas de muchos elementos, como los cristales y el hielo, en las olas de la playa se dan espirales logarítmicas, en las corrientes oceánicas, en las estrellas marinas, tanto en su disposición en forma de pentagrama como en sus protuberancias, en el crecimiento de los árboles, en las piñas de los pinos, en la estructura de las conchas, como por ejemplo el nautilo, en los pétalos de las flores, en las espirales de las galaxias, en los elementos de los girasoles, en el crecimiento de las hojas, en la espiral del ácido desoxirribonucleico, en los latidos del corazón, etc. No hay nada misterioso en la aparición de esta proporción en la naturaleza, su existencia se debe a que casi todos los elementos geométricos aquí nombrados tienen una estructura pentagonal regular, mientras que en la naturaleza se debe a que los organismos utilizan siempre una disposición que facilita su orientación hacia el sol, como es el caso del orden de las hojas de la palmera o de las escamas de la piña o de las pipas del girasol que se van distribuyendo en torno a la circunferencia mediante la proporción áurea para aprovechar mejor el espacio. Tanto los pétalos de una flor como su distribución por los tallos de las plantas siguen la proporción áurea ya que de esta manera pueden tener acceso fácil a la luz, y evitar el solapamiento de pétalos u hojas según se van distribuyendo por el tallo, siempre siguiendo las pautas de la proporción áurea. Por un lado, la geometría pentagonal determina la aparición de la proporción áurea en numerosos elementos geométricos, mientras que por otro lado los elementos naturales buscan al aprovechar la luz y el espacio ésta disposición. Existe cierta afinidad entre esta proporción y las simetrías, los elementos naturales también se someten a la búsqueda continua de simetrías, así por ejemplo una pompa de jabón buscando un estado de mínimo consumo energético se compacta hasta aparecer como una esfera. La estructura interna de los diamantes para tener una disposición más resistente se organiza mediante tetraedros de carbono, los virus se replican más fácilmente al adoptar formas con multiplicidad de simetrías ya que éstas facilitan además una mayor resistencia para su integración en la célula.
En general, en la naturaleza se da la proporción áurea para aprovechar los recursos naturales como pueden ser el sol; así el crecimiento de los pétalos o los elementos de una piña o de una flor como el girasol crecen a 137,5° respecto al último elemento, pues el arco del sector azul b y el del sector amarillo a están en proporción áurea. El arco completo de la circunferencia de 360º dividido entre 1,618 es igual a 222,5º, (el sector azul), lo que queda o sector de color amarillo se obtiene al restarle 222,5º a 360º, que es igual a los 137,5º, el ángulo de crecimiento de las hojas.
 Los 137,5°, como se puede ver en la imagen, evitan el solapamiento desde el nº 1 al 20 sobre la misma circunferencia, para ello se disponen los elementos en disposición de espiral o hélice cuando es una distribución tridimensional, como las ramas de un tallo. En la naturaleza el crecimiento con este ángulo permite que el pétalo u hoja que sale respecto a los anteriores pueda disponer de la luz del sol sin ser solapado o interferido por los otros, el 1º es el 0, el 2º el 1, etc. Además de la disposición angular de 137,5º, el crecimiento se hace sumando desplazamientos desde el centro hacia afuera, con lo que la disposición es en espiral. Los 137,5°, como se puede ver en la imagen, evitan el solapamiento desde el nº 1 al 20 sobre la misma circunferencia, para ello se disponen los elementos en disposición de espiral o hélice cuando es una distribución tridimensional, como las ramas de un tallo. En la naturaleza el crecimiento con este ángulo permite que el pétalo u hoja que sale respecto a los anteriores pueda disponer de la luz del sol sin ser solapado o interferido por los otros, el 1º es el 0, el 2º el 1, etc. Además de la disposición angular de 137,5º, el crecimiento se hace sumando desplazamientos desde el centro hacia afuera, con lo que la disposición es en espiral.
En la imagen podemos observar a la izquierda un rectángulo áureo FEBD y a la derecha un triángulo áureo NOP. Si al rectángulo áureo le quitamos un cuadrado CFEA (en color amarillo) el rectángulo que queda ABCD es idéntico en su forma al rectángulo original FEBD, se dice que son proporcionales (igual forma y distinto tamaño). Si sobre el verde quitáramos otro cuadrado el que quedaría también sería idéntico al original en su forma. Esta es una peculiaridad que se da sólo en los rectángulos áureos.
En la imagen de la derecha observamos un triángulo áureo NPO, análogamente si se le quita un triángulo isósceles PMO, (en la imagen en color amarillo) el triángulo MNO que queda en color verde es idéntico al triángulo original NPO. De igual forma podríamos quitar al triángulo verde otro triángulo isósceles y nos quedaría al restar éste otro triángulo idéntico en su forma a los dos anteriores.

Para construir un rectángulo áureo dado el segmento medio AB de la proporción, en el punto medio P de la base de la figura AB hacemos centro con un arco cuyo radio va desde ese punto P hasta cualquiera de los dos vértices superiores del cuadrado, por ejemplo el punto Q. Donde ese arco corta a la prolongación del lado de la base AB tenemos el nuevo punto C que determina con B el segmento BC, que está en proporción áurea con el anterior AB. Si sobre este segmento BC dibujamos un rectángulo con la misma altura que el cuadrado (en el dibujo en color amarillo) , tenemos un rectángulo áureo. Esto quiere decir que el nuevo rectángulo amarillo es proporcional al rectángulo formado por el rectángulo amarillo más el cuadrado azul, ya que el segmento mayor es al medio como el medio es al menor.
Demostración: tenemos que demostrar que el segmento mayor AC es al medio AB como el segmento medio es al menor BC. Gráficamente lo podemos expresar mediante dos triángulos semejantes: el triángulo AMC y el triángulo ABN.
Observamos que el segmento mayor AC se transforma en el segmento medio MA o lado del cuadrado AB, ya que MN =AB. Ahora transformamos el segmento AB en el segmento NA mediante una recta paralela BN a MC.
Se trata de demostrar que el segmento NA tiene que ser igual a BC, para que se verifique el teorema de la proporción áurea. Haciendo una circunferencia con centro en el punto medio de la base del cuadrado O observamos que esta pasa por el punto C y por el punto K, de ello se desprende que el segmento BC es igual al segmento KA, pero éste también es igual al segmento NA, con lo que queda demostrado que AC es a MA (o AB) como MA que es a NA (o BC).
En el dibujo podemos observar un rectángulo áureo formado por un cuadrado en color amarillo y otro rectángulo áureo en color azul. Al segmento mayor del rectángulo se le ha dado el valor 1,618, por lo que tenemos que el segmento medio vale 1 y el segmento menor vale 0,618. De esta forma tenemos que el segmento mayor es al medio, (esto es, 1,618 dividido entre uno es igual a 1,618, por lo que tenemos ya el número de oro ), como el segmento medio, esto es, uno es a el segmento menor, 0,618. De ello se desprende que uno dividido entre 0,618 es igual a 1,618, ya que existe la misma proporción entre el segmento medio y el menor que entre el mayor y el medio. Esto se puede expresar gráficamente de la siguiente forma:
En cada rectángulo áureo consideramos la proporcionalidad que existe mediante otro rectángulo áureo menor. El rectángulo áureo mayor, determinado su segmento mayor por los puntos AC, se transforma en otro rectángulo áureo menor cuyo segmento mayor es A’B’. Pero al mismo tiempo este segmento mayor corresponde al segmento medio A’B’ del rectángulo anterior.Como podemos observar, los rectángulos áureos se van repitiendo hasta el infinito de manera que el segmento medio de cada rectángulo áureo es el mayor del siguiente, y según la progresión, el menor del primero se transforma en el medio del siguiente con lo que se hace patente la relación de proporcionalidad entre los tres segmentos: grande, medio y menor.
Para calcular la proporción áurea de un segmento dada la dimensión mayor DC de la proporción, se hace un arco con centro en el extremo del segmento C y con radio AC siendo este la mitad del segmento DC. El arco corta a la vertical por C en el punto B. Unimos el punto B con el otro extremo del segmento D y hacemos centro en B con el radio BC hasta que corta al segmento DB en el punto P. Hacemos un arco con centro en el punto D y con el radio DP hasta que corta al segmento DC en el punto S, este punto define la división del segmento mayor DC entre el medio DS y el menor SC.
En la figura podemos observar las tres circunferencias que hay que hacer para dividir el segmento mayor de la proporción áurea en los otros dos. Primero hacemos la circunferencia amarilla con el centro en el extremo del segmento, luego la circunferencia azul tangente a la base otra vez en el extremo del segmento y por último la circunferencia naranja, tangente a la circunferencia azul y con el centro en el otro extremo del segmento.
Si tenemos un segmento AB que queremos
dividirlo según la proporción áurea, construimos una línea perpendicular por el
extremo B y tomamos sobre esta la mitad de la dimensión de AB.
BC=1/2 (OB)
Construimos una circunferencia naranja de
radio CB sobre la recta perpendicular, de esta manera tenemos una
circunferencia tangente a la línea dada que corta a la recta OC (unión del
centro de la circunferencia con el extremo del segmento dado) en el punto A.
Tomando ahora centro en el punto O y como
radio la distancia OA construimos un marco (en color amarillo) hasta que corta
a la línea OB en el punto G. de esta manera hemos dividido AB según la proporción
áurea. Tenemos por tanto que OB/OG=OG/GB.
El fundamento de esta construcción reside en
la potencia de un punto O respecto a la circunferencia naranja. Tenemos que
para cualquier secante que incida sobre el centro O, lo siguiente:
OA.OA’= constante
La posición límite de cualquier secante en la
circunferencia es una recta tangente que transforma los dos puntos de corte con
la circunferencia en uno, de esta manera el punto homólogo de B es B’, un punto
doble que se ha transformado en sí mismo.
Tenemos por tanto que OA.OA’= OB.OB’= k.
Si pasamos OA al denominador del segundo término
y pasamos OB’ al denominador del primer término tenemos que OA’/OB’=OB/OA, que
no es otra cosa que la proporción áurea entre OA’ OB’
y OA.
También podemos dividir un segmento en proporción áurea mediante proporcionalidad, dado el segmento mayor AB.
Dado un segmento AB, se trata de determinar dónde queda el punto C. Construimos una línea cualquiera v que pase por A. Sobre un punto M de esta recta hacemos el segmento MO paralelo al anterior AB. Calculamos el punto N por el procedimiento anterior y tenemos un rectángulo a áureo con la proporción MN/MO=MO/ON.
Alineamos el punto B con el punto N y tenemos en la intersección con la recta v el centro de proyección P. Construimos una recta que pase por los puntos PO y donde corte su prolongación al segmento AB obtenemos el punto buscado C.
En la figura observamos mediante un giro y traslación a la base que la dimensión menor BC del rectángulo áureo ABC se corresponde con la media del siguiente A'B' correspondiente a A'B'C'. De esta forma observamos que el mayor al medio como al medio al menor se corresponde nuevamente, el medio pasa a ser el mayor y el menor en medio, una correspondencia constatada de forma gráfica.
Si cogemos una manzana, podemos observar que sus semillas están configuradas según una estrella de cinco puntas, figura llamada en geometría pentagrama, y esta figura no es otra cosa que un pentágono al que se le han añadido triángulos isósceles a sus lados. Los vértices alternos de este pentagrama están en proporción áurea con respecto a el lado del pentágono donde se inscriben. Las diagonales del pentágono definen el pentagrama y en el centro del mismo otro pentágono en el que se puede dibujar otro pentagrama invertido y así hasta el infinito. En la proporción áurea se da una progresión continua cuyo cociente es siempre el número de oro.
 Si unimos los vértices de un pentágono entre sí mediante todas sus diagonales obtenemos el pentagrama (en el dibujo en color violeta). Cada diagonal del pentagrama, o recta que une cada par de vértices opuestos del pentágono, está en proporción áurea con el lado del pentágono regular. Si unimos los vértices de un pentágono entre sí mediante todas sus diagonales obtenemos el pentagrama (en el dibujo en color violeta). Cada diagonal del pentagrama, o recta que une cada par de vértices opuestos del pentágono, está en proporción áurea con el lado del pentágono regular.
En un pentagrama el triángulo ABC se llama triángulo áureo y es aquel triángulo isósceles cuyo lado desigual está en proporción áurea respecto a cualquiera de los otros dos lados. En la figura el triángulo de la izquierda formado por los fragmentos amarillo y naranja es un triángulo áureo. Los brazos verdes del pentagrama también son triángulos áureos.
En la figura de la derecha observamos una espiral construida a partir de este triángulo áureo, dentro del primer triángulo se ha puesto otro menor girado y dentro de este otro y así hasta el infinito. De esta manera en cada triángulo tenemos una circunferencia correspondiente al primer arco con centro en el punto 1 y arco 1, a continuación tenemos otra circunferencia con centro en el punto 2 y arco número 2 y así sucesivamente. El enlace de todos estos arcos de circunferencia determinan la espiral.
En los dos dibujos del pentágono observamos que el pentágono y algunos segmentos del mismo están en proporción áurea.
En la figura de la izquierda tenemos que AC/AB=AB/BC y AB/BD=BD/DA
En la figura de la derecha tenemos que la diagonal EG del pentagrama y el lado del pentágono EF están en proporción áurea y EG/EF=EF/FG pero FG=HG y
GI/GH=GH/HI por lo que EG/EF=EF/HG.
En la figura de la izquierda tenemos que MP/MO=MO/OP y como el segmento PO es igual a NO tenemos que en el pentagrama MP/MO=MO/ON.
En la figura de la derecha observamos que al girar un lado del pentágono hasta hacerlo coincidir con la diagonal JK del mismo, ambas (JK y KL) están en proporción áurea.
Si construimos un pentágono regular p inscrito en una circunferencia c y hacemos la mediatriz m de uno de sus lados, cortará a la circunferencia en un punto T que unido al vértice más cercano del pentágono define el lado a del nuevo polígono regular: un decágono regular. El lado del decágono regular a está en proporción áurea con el radio de la circunferencia b en la que se inscribe:
b+a’/b= b/a’
y a’=a
En la figura observamos un poliedro arquimediano obtenido por el corte de un dodecaedro o un icosaedro. Este poliedro arquimediano se llama icosidodecaedro y observamos que en su proyección ortogonal estos segmentos del mismo están en proporción áurea.
Dentro de un triángulo isósceles siempre se puede hacer otro triángulo semejante (de igual forma aunque de distinto tamaño).
En el vértice b del triángulo mayor hacemos la recta perpendicular m al lado opuesto. Dibujamos la recta simétrica s’ de la base s respecto al eje m y ya tenemos un triángulo de igual forma aunque de distinto tamaño, ya que el ángulo c es común a ambas triángulos, y ya que acabamos de calcular el ángulo d simétrico e igual al anterior y como el triángulo mayor también tiene el ángulo e simétrico al ángulo c, tenemos que los ángulos a b son iguales.
Como podemos comprobar no es un triángulo áureo ya que el lado desigual y uno de los lados iguales no están en proporción áurea, si lo fuera, al restar el mayor del menor quedaría un triángulo isósceles (de 2 lados iguales). El triángulo abd tendría que ser isósceles para ser áureo.
En la figura de la derecha podemos observar el triángulo áureo ABC, determinado por dos diagonales y un lado del pentágono. Según la construcción que acabamos de ver, el triángulo BCD es semejanteal anterior. De igual forma el triángulo BDE también es semejante al anterior, ello es debido a que todos los segmentos de los pentagramas interiores y del pentágono están en proporción áurea.
En la figura de la izquierda comprobamos que esto es cierto, en la ilustración aparecen segmentos que determinan proporciones áureas, por ejemplo ABC, DEF,GHE, HIJ,etc. , los determinados por los cuadrados azules y arcos ocres.

En la figura observamos una espiral construida sobre rectángulos áureos. En cada cuadrado hacemos un arco de circunferencia cuyos extremos estén en la diagonal o vértices opuestos y cuyo centro este en el vértice de la otra diagonal. De esta manera hacemos centro primero en el punto uno, luego en el dos, luego en el tres, y así sucesivamente. Cada arco es tangente al cuadrado y al arco adyacente y ocupa el cuadrado de cada rectángulo áureo. En la siguiente página podemos observar figuras planas construidas con la sección áurea: curvas planas
 En la figura observamos el icosaedro y dodecaedro, vamos a explicar su construcción ortogonal en sistema diédrico (consultar el sistema diédrico en el apartado de figuras) teniendo en cuenta su relación con la proporción áurea: En la figura observamos el icosaedro y dodecaedro, vamos a explicar su construcción ortogonal en sistema diédrico (consultar el sistema diédrico en el apartado de figuras) teniendo en cuenta su relación con la proporción áurea:
En la figura podemos observar la relación de la proporción áurea con dos poliedros regulares: el icosaedro y el dodecaedro. La arista del icosaedro más la arista del dodecaedro es igual a la arista del cubo en el que se inscriben y las tres dimensiones están relacionadas mediante la proporción áurea, siendo la mayor la arista del cubo, la dimensión media la arista del icosaedro y la menor la del dodecaedro.
En la parte superior del dibujo, sobre el lado del cuadrados tenemos el rectángulo áureo compuesto por el cuadrado verde cuyo lado es el del icosaedro y el rectángulo amarillo cuyo lado de la base es el del dodecaedro. Observamos que ambos lados suman el lado del cuadrado en el que se inscriben el dodecaedro y el icosaedro.
Podemos observar además que si tomamos el punto medio N de la base del cuadrado verde y lo unimos con el vértice S (punto medio en la cara del cuadrado) tenemos la proyección SN de una cara del dodecaedro.
Si alineamos el centro N de la base del cuadrado AB con el vértice S obtenemos un vértice del dodecaedro T en la intersección de esta línea con la diagonal AU. Haciendo una recta vertical por el vértice T obtenemos el vértice del icosaedro, ya que ambas dimensiones son iguales, la diagonal del pentágono del dodecaedro y la arista del icosaedro.
En la figura podemos observar varios poliedros estrellados, dos de los cuatro de Képler-Poinsont. Podemos observar en sus proyecciones diédricas como los elementos están relacionados mediante múltiples proporciones áureas. Ello es debido a que éstos poliedros estrellados están íntimamente relacionados con los pentágonos regulares, de ahí sus nombres.
En la figura podemos observar las proyecciones ortogonales de los dos poliedros estrellados de la figura anterior. En estas vistas las proyecciones de algunos vértices están también en una relación áurea: GI/GH=GH/HI, JL/JK=JK/KL y AC/BC=BC/BA, DF/DE=DEEF.
En la gran pirámide de Egipto de Ghiza, la relación entre sus caras y la altura de la misma es una proporción áurea. El área de cada cara equivale al área de un cuadrado cuya altura corresponde al de la pirámide, esto quiere decir que una cara triangular de la pirámide es equivalente al cuadrado que tiene como lado la altura de la pirámide. Si tomamos una cara de la pirámide y cogemos la altura de la misma y la dividimos por la mitad del lado de la base de esa cara tenemos como cociente el número de oro.
Hay muchos y diversos estudios que relacionan la proporción áurea con las pirámides de Egipto, en general todos hacen cálculos aproximados de esta relación sobre las mismas, sin que haya absoluta certeza de que hubieran utilizado este dato conociendo la proporción áurea, pudiendo ser un cálculo fruto del azar.
En la figura tenemos la gran pirámide de Egipto, sobre cualquiera de sus caras triangulares tenemos que la altura del triángulo n y la mitad del lado de la base p están en proporción áurea: n/p=1,618. (n+p/n=n/p).
Si al área de esta cara triangular le llamamos B y a la de la base de la pirámide le llamamos A tenemos que sumando las áreas de las cuatro caras triangulares y dividido este número por el área del cuadrado de la base obtenemos 1,618, el número de oro.
Si sumamos las áreas de las caras triangulares al área de la base de la pirámide y todo ello lo dividimos entre la suma de las áreas de las caras triangulares obtenemos también el número de oro, 1,618. (4B+A)/4B =1,618.
Si calculamos la altura de la pirámide desabatiendo cualquier cara triangular hasta que el vértice del triángulo corte a la altura de la pirámide veremos que la altura de la pirámide es el lado de un cuadrado cuya área C es igual al área del triángulo de cualquier cara B. En geometría se dice que el triángulo y cuadrado son equivalentes, que tienen la misma área. C=B.
En la figura podemos observar cómo construir la altura de la pirámide dada en planta. Como conocemos el lado y la altura de la cara triangular la colocamos coincidente con el plano de la planta. La proyectamos sobre el alzado y haciendo un giro con centro en O2 con radio O2-A2, donde corte al eje e de la pirámide obtenemos el vértice superior S, de esta manera obtenemos el lado del cuadrado L equivalente a la cara triangular. Como podemos observar con el abatimiento, la altura de la figura queda totalmente establecida a partir de las caras de la pirámide.
Gráficamente podemos calcular un cuadrado equivalente a un triángulo de la siguiente forma: dado el triángulo amarillo ABC, por el punto medio de su altura se hace un rectángulo GPBC con esa altura y con la misma base BC. Se hace una circunferencia del centro P con radio GP obteniendo sobre la prolongación de PC el punto J, intersección de este se segmento con la circunferencia. Construimos otra circunferencia de diámetro PJ y donde la prolongación del lado BC corta a la circunferencia (en O), lo unimos con P. El segmento PO es el lado del cuadrado (en color azul) equivalente al triángulo dado. Demostración en la página : Figuras equivalentes
En la figura tenemos un triángulo rectángulo cuyos lados m n o están en progresión aritmética (se puede obtener uno a partir del otro mediante adicción o suma) y es conocido como triángulo egipcio, otras veces conocido como triángulo de Plutarco o de Pitágoras, sus dimensiones son 3, 4 y 5, o bien segmentos proporcionales a éstos.
Si restamos la hipotenusa n menos un cateto m obtenemos la dimensión b, si le restamos a un cateto m el otro cateto o, obtenemos la dimensión a. Podemos comprobar que el segmento a tiene la misma longitud que el segmento b y ello se expresa gráficamente al girar el segmento b hasta transformarlo en el segmento c paralelo al segmento a. Mediante una traslación se comprueba que los segmentos a y c son idénticos. Por tanto en este triángulo la hipotenusa menos un cateto es igual a un cateto menos el otro: n-m=m-o.
Una de las pirámides de Gizéh tiene este triángulo en su sección mediana, aunque este triángulo no tiene relación con el número de oro, el triángulo de la sección meridiana de la gran pirámide sí que lo tiene y es el que describimos a continuación:
Si construimos un cuadrado ABCD y a partir de su base AD obtenemos el nuevo segmento en proporción áurea DK, por el punto medio del segmento AK hacemos una semicircunferencia s, en la prolongación del segmento DC obtenemos con la intersección de esta semicircunferencia el punto J. Este triángulo que obtenemos AJK es el que corresponde al semiperfil meridiano de la gran pirámide. Si ahora a partir de la hipotenusa AK construimos otro cuadrado AKEF y su correspondiente segmento que está en proporción áurea con él, esto es, el segmento KH, comprobamos que haciendo centro en el punto K y tomando como radio JK, verificamos que el segmento KH es igual al segmento JK.
Tenemos por tanto que los segmentos AD y DK y los segmentos AK y JK están respectivamente en proporción áurea, ya que JK=KH, y que por tanto AD/DK=AK/JK.
La serie de Fibonacci: Leonardo de Pisa, hoy conocido con el nombre de Fibonacci, hizo un interesante descubrimiento: construyó una serie numérica empezando por el 0, 1,1,2,… a partir de estos números empezó a sumar siempre los dos últimos: 0,1, 1,2,3, 5,8, 13,21,…(1 más 2 igual a 3, 2 +3 es igual a 5, 3 + 5 igual a 8, 5 + 8 es igual a 13, etc.) aunque no se sabe si conocía la relación que tiene esta serie con la proporción áurea, (según avanzamos, el cociente entre los 2 últimos se aproxima cada vez más al número de oro), sí se conoce que en el siglo XIII había planteado esta serie en base a la relación con la cría de los conejos.
Los números naturales son 1,2, 3,4, 5,6,… son todos números enteros. Son enteros también el cero y los números negativos, y se pueden expresar mediante el cociente entre dos enteros, salvo alguna excepción. Se pueden expresar también de forma fraccionada o con decimales, son números reales, o sea no imaginarios. Los números irracionales no se pueden expresar como razón de números enteros y su desarrollo mediante decimales es infinito, como por ejemplo raíz de dos, o raíz de tres, etcétera. La raíz de dos tiene por valor 1,41421356237…, un conjunto de números que nunca se repiten, al igual que el número de oro –phi- también es un número irracional y real. Los números reales, sean racionales o irracionales son los que corresponden a los puntos de una línea infinita.

Si hacemos rectángulos con los números de Fibonacci, y los adherimos unos a otros en una disposición vertical y en espiral como muestra la figura, el contorno de los rectángulos es un cuadrado perfecto. De igual forma al empezar a disponerlos de mayor a menor, el azul, a continuación el violeta, después el rojo y el naranja, observamos que queda un hueco cuadrado que podemos ir llenando con nuevos rectángulos hasta el infinito.
Vídeo sobre la proporción áurea: http://www.youtube.com/watch?v=d_7I-uqz_ic&feature=related
|
P. áurea |
En la imagen derecha correspondiente al círculo verde podemos
observar cómo transformamos el segmento mayor AF en el segmento medio AD (que es igual al segmento AB por ser la figura
que los contiene un cuadrado) y AB en el segmento menor AG. Podemos verificar
que es cierto, que AG es el segmento menor pues haciendo centro en el punto A y
tomando como radio la distancia GA obtenemos el punto H en la intersección con
la prolongación del segmento AF. Como el cuadrado está centrado en la
circunferencia tenemos que el segmento HA es igual al segmento BF, con lo que queda
demostrada la relación de proporción áurea: AF/AB=AB/BF, y AF=AB+BF.
En la imagen izquierda podemos observar una figura análoga
pero demostrando la proporción áurea mediante
otra transformación: el segmento mayor IN se transforma en el segmento medio
IJ, o también IL y el segmento medio IJ se transforma en el segmento menor IQ
mediante proyecciones paralelas, haciendo uso del teorema de Tales.
Si por J hacemos una recta paralela al segmento NL obtenemos en la vertical por I el punto Q que lo tomamos
como centro de una circunferencia de radio QI. En consecuencia el segmento
menor QI es igual al segmento QR y tenemos que si trasladamos el segmento menor
JN según la dirección JQ tenemos que se transforma mediante una traslación en
el segmento QR. De esta forma podemos comprobar la transformación mediante el
teorema de tales en la que se puede comprobar que el segmento mayor IN es al
segmento medio PO, como el segmento medio es al segmento menor QR.
De la última relación anterior se deduce que los segmentos NO y OR están en proporción áurea, de la misma forma y conforme al teorema de Tales tenemos que también están en proporción áurea los segmentos IP y PQ.http://proporcion-escala-semejanza-homotecia.blogspot.com.es/
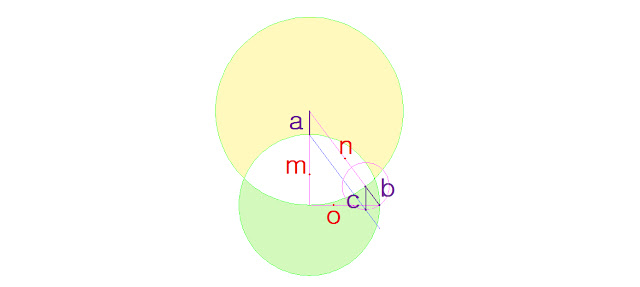
El número de oro al cuadrado es igual al número
de oro +1.
En el dibujo tenemos que, según el teorema de
la altura, el triángulo de catetos a b y el rectángulo amarillo de lado mayor
c, la siguiente relación: el segmento menor a es al segmento medio b, como éste
lo es al mayor c. Además podemos comprobar que el segmento mayor c es igual a
la suma de los otros dos a+b. Esto se puede verificar en el dibujo de la
siguiente manera, el segmento a este lado del cuadrado de color rosa de una
unidad sumado al segmento b define el radio de la circunferencia verde i, como
podemos observar es el lado mayor c del rectángulo amarillo, que no es otra
cosa que el lado b+1 o el lado b+a, ya que es igual a uno.
En consecuencia hemos dibujado el teorema de
la altura tomando como dimensiones los segmentos correspondientes a la proporción
áurea, a/b=b/c y c=a+b.
Como a/b=b/c tenemos que b es media
proporcional entre los segmentos a y c. Y como el producto de medios es igual
al producto de extremos tenemos que a.c=b.b.
Pero como a vale la unidad tenemos que b al
cuadrado es igual a c. Pero según se vio anteriormente, el radio de la
circunferencia es b+1, en consecuencia b al cuadrado es igual a b+1.
En el dibujo tenemos por tanto que a=1, b es
igual a 1,618 (el número de oro) y c es igual a 1,618 + 1, esto es 2,618. Este
es el valor también del número de oro al cuadrado, como se acabó de demostrar.
Los fractales
Un fractal es una estructura repetitiva a distintas escalas, como pasa con la proporción áurea que cuando se repite a distintas escalas lo hace siempre de forma autosemejante o autosimilar. Por ejemplo, la geometría fractal natural de una galaxia es al mismo tiempo de tipo áureo, pues a parte de ser autosimilar sigue los parámetros de la proporción áurea.
Los fractales
Un fractal es una estructura repetitiva a distintas escalas, como pasa con la proporción áurea que cuando se repite a distintas escalas lo hace siempre de forma autosemejante o autosimilar. Por ejemplo, la geometría fractal natural de una galaxia es al mismo tiempo de tipo áureo, pues a parte de ser autosimilar sigue los parámetros de la proporción áurea.

































